いろいろ 数学 順列 問題 178567-数学 順列 問題
今回の問題は、「生徒 全員 を1列に並べる」場合の数を求めるんだね。「異なる n個 のものを すべて1列に並べる ときの場合の数」は、「 nの階乗 」といい、「n!=n×(n1)×(n2)××3×2×1」で計算練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理,チェバの定理隣り合う円順列の問題は まず $1$ つにまとめてしまい、円順列の総数を求める。 $1$ つにまとめたもの同士の並び替えの場合の数を求める。 積の法則より、掛け算すればok;

数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube
数学 順列 問題
数学 順列 問題-今回は数学Aの順列Pの公式と使い方についてサクッとまとめました。 順列 異なる 個のものから異なる 個を取り出して並べるときの並べ方 順列のはむずかしいものではないので、たくさん問題に挑戦すればきっとできるようになります。 順列と 順列の特訓プリントです (`・ω・´) 図を描くのが解くためのカギです (*´ω`*) 数学A 順列 人を並べる特訓① 数学A 順列 桁数問題特訓① 数学A 順列 辞書式配列・小さい順特訓① 数学A 順列 円順列 (人を並べる)特訓① 数学A 順列 円順列 (図形の色塗り)特訓① 数学A 順列 重複順列特訓① スポンサードリンク




順列pと組み合わせcの違いと 簡単 な見分け方
前回 https//wwwyoutubecom/watch?v=gkeQK_kfa5w 次回 https//wwwyoutubecom/watch?v=4LJtn7VG67Mサブチャンネル とある男がゲームを高校数学A この教材を使う際は 問題を解いて解答が一致した後,一応解答をチェックすることをお勧めします. 「重複を許す」,「順列例題 (1) 両親と子供 4 人の 6 人が円形のテーブルに向って座るとする。 次のような座り方は何通りあるか。 ( ア ) 6 人全体の座り方 ( イ ) 両親が隣り合わない座り方 ①異なる n 人 ( n 個 ) を並べる円順列は で求めよう。 ②隣り合わないときは余事象,または間に入れよう。 (1) ( ア ) 6 人の円順列の総数より ( 通り )
問題を読んでも、順列と組合せのどちらの式を利用すればいいかわからない。ということですね。 解説 まず、順列と組合せについて正しく理解しましょう。 《順列》 一般に、いくつかのものを、順序をつけて1列にならべた配列を順列と いうのでしたつまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ 問題 5人がそれぞれプレゼントを持ち寄り,それらを無作為に1つずつ再分配してプレゼント交換するとき,5人すべてが自分のプレゼントと異なるプレゼントを受け取る場合は何通りあるか. カテゴリー 場合の数, 数学a タグ 完全順列, 数学
では、順列pの計算についての理解が深まっているかどうか練習問題に挑戦してみましょう! 次の計算をしなさい。 (1)\({}_8 \mathrm{ P }_4\) 応用問題 ←解答 順列 基本問題 ←解答 応用問題 ←解答 円順列と重複順列 基本問題 ←解答 応用問題 ←解答 組合せ 基本問題 ←解答 応用問題 ←解答 同じものを含む順列 基本問題 ←解答 応用問題 ←解答解答と解説 『順列・組合せ』の問題の解き方や、使う公式に関しては『spi 順列・組合せ ~練習問題と解き方を徹底解説!~』のページで詳しく解説しています。解き方が分からない方は、まず、そちらのページを一読してください。




高校数学のサイコロの問題と順列の問題と順列の利用 Clear




場合の数 怜悧玲瓏 高校数学を天空から俯瞰する
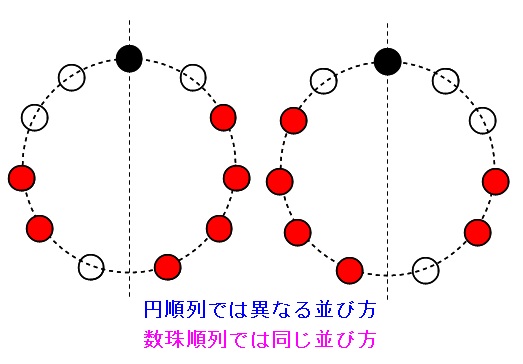
おすすめの数学クイズ傑作問題まとめ!算数レベル〜超難問 おもしろい算数・数学パズルを集めました。 小学生でも解けるものから、中学・高校生はもちろん大学生すら苦労するものまで。 頭をひねる面白い数学クイズの世界を楽しんでください! 順列・組み合わせで解けるけれど,どう解いてよいのか迷う人が多そうな問題を集めてみました。すべて「順列作戦」と「組み合わせ作戦」の2通りの解法を用意してありますので,頑張って挑戦してみてください。 例題1 \(aaabb\) の並 じゅず順列の問題です。まずは基本問題から。 1. 互いに異なる7つの玉がある.これらの玉を糸でつないで首飾りをつくるとき,何種類の首飾りを作ることが可能か. 次に線対称な円順列を含むじゅず順列の問題



高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com
攪乱順列のことを 完全順列 とも言います。攪乱順列の方が漢字は難しいですが,意味は分かりやすいと思います。 n n n 個の場合の攪乱順列の数 a n a_n a n は モンモール数 とも呼ばれます。 モンモール数を求める問題は モンモールの問題 とも呼ばれます。 高校数学無料問題集 数A 第1章場合の数と確率②順列 この講から、本格的な場合の数の問題に入っていきます。 まずは順列。 教え方がマズいと、「Pなの? Cなの? 」といういけてない疑問が生じますが、Pはただの省略の記号であって、考える上で中学数学の問題ソフト無料 中1数学 正負の数,文字と式,1次方程式,比例・反比例,平面図形,空間図形,資料の活用 中2数学 式の計算,連立方程式,1次関数,図形の性質,確率 中3数学 式の計算,平方根,2次方程式,2次関数,相似な図形,円周角,三平方の定理,標本




高校数学 数a 勉強動画 順列 続 基本編の問題 19ch




数学ia 同じものを含む円順列 数珠順列 大学入試数学の考え方と解法
順列と組合せの応用問題5選 それでは、ここからは順列と組合せの応用問題をごちゃまぜに $5$ 問解いていきたいと思います。 具体的には 委員の選出;円順列の問題の考え方 例 黒,赤,青,緑の 4 4 色の玉を円状に並べるのは何通りか. 円順列の問題のポイントは, 回転して同じものは同じ並べ方としてみる という点にあります. それを踏まえると,以下の 6 6 通りになります. 問題を解く上で,回転されると手に負えないので, 回転を止めて考える のがポイントになります. 黒が上にあるときで固定して 重複順列の考え方を応用して,組分けの問題を解いてみましょう. 例題 赤,青,黄,緑,紫色の 5 5 つの球がある. (1) 5 5 つの球を 2 2 つの箱 X,Y X, Y にいれる方法は何通りあるか.ただし,ひとつの球も入っていない箱があってもよいとする. (2) 5 5 つの




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



最短経路 の指導法 怜悧玲瓏 高校数学を天空から俯瞰する
数学・算数 順列の問題がわかりません。教えてください。 順列の問題を教えてください。 a,b,c,d,eの5文字すべてを並べて順列を作る。 (1)一番左の文字がaである順列は全部で何個あるか。 質問Noじゅず順列の問題の考え方 黒,赤,青,緑の4色の玉をじゅず状に並べるのは何通りか. じゅず順列では, 3次元空間内の輪として同じものは同じ並べ方としてみます .つまり円順列において, 裏返して同じものは同じ並べ方とします . それを踏まえるについてパターン別に解説していきます。 取り上げる問題はこちら! 問題①(0を含まないパターン) 6個の整数 , , , , , から異なる3個の数字を選んで3桁の整数をつくるとき,次のような数の個数を求めよ。 (1)すべての整数 (2)偶数 (3)4の



その他の確率の問題 Of 京極一樹の数学塾会員頁




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら
例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り 例 2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から重複を許して2つを取って並べる順列 10Π2 =10 2 =100 練習問題 順列と組合せの問題を混ぜました。順列と組合せの違い 順列 :「選んで並べる」「abとba を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「abとbaは区別せず同じもの」 に注意しながら,考えてみてください。 ここでは「順列」について説明します。順列とは,いくつかあるものを順序をつけて1列に並べる配列のことです。意味を考えて順列を求めるヒロ例えば次の問題を考えてみよう。問題a, b, c, dの4人がリレーをするとき,走る順番は何通りあるか。ヒロ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




苦手な人向け 順列pの計算のやり方を簡単にサクッと解説するぞ 数スタ
順列・組合せ総合問題 練習問題19 5人の旅客が3件の旅館に泊まる泊まり方は何通りあるか。 ただし1人も宿泊しない旅館があってもよいとする。 上の問題において,人を仮に固定し,どの旅館に宿泊するか,ということを考えればよいのです。 発想のつまり、順列の問題とは、 「 n個の要素を、r個の異なる席に当てはめる場合の数 」を求める問題、と言えます。 基礎的な問題では、「要素の並べ替え」でも「席に当てはめ」でも ほとんど変わらないように思えるかもしれませんが、 1番目はn個のどれでも可能なので n通り 2番めは1番目で取った残りが (n1)個なので (n1)通り ・・・ (順に1つずつ減るので)・・・ 3番めは (n2)通り ・ 10番目は (n9)通り ・ r番




高校数学 数a 勉強動画 順列 男女編の問題 19ch




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
数学 はるにゃんこ 3分で分かる!順列と組み合わせの違いと公式をわかりやすく(練習問題つき)10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り詳しくは順列・組合せの問題の見分け方のページを見てね。 積の法則 事象Aとなる場合が `n_A` 通りあり、 "Aが実際にどうなったかに関わらず" 、事象Bとなる場合が `n_B` 通りあるとき、事象A、Bがともに起こる場合は `n_A xx n_B` 通りある。




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




順列の問題 一定の条件で並べる 高校数学の知識庫



確率問題全般 京極一樹の数学塾




数学コラム第4回 エッセンス 筑駒中 の順列問題のおさらい まっちゃんスター 数学エッセンスクラス Note



順列の青チャートの問題なんですがここの 3 の 2 の説明が全く分かり Yahoo 知恵袋




数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法



プレゼント交換会の数学 完全順列 理系男子の独り善がり




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




順列と組み合わせ 算数用語集




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門



Q Tbn And9gctdg7qzyj8jefiumjmojygwqcr6bhmbi685zwhir13rni5bkqx6 Usqp Cau




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




Spi 数学 対策問題 推論 順列 しかくのいろは




高校数学のサイコロの問題と順列の問題と順列の利用 Clear




高校数学 数a 勉強動画 順列 グループ分け編の問題 19ch




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




数学コラム第4回 エッセンス 筑駒中 の順列問題のおさらい まっちゃんスター 数学エッセンスクラス Note



12 鹿児島大学 入試問題から Kadaiの順列




順列 数学a 高校1年生 1学期中間考査ワーク練習問題 赤城 ᐡᐤᐡ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



円順列と数珠順列の考え方や公式と問題の解き方




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




攪乱順列 完全順列 の個数を求める公式 高校数学の美しい物語




3講 順列 1章 場合の数と確率 問題集 高校数学a




高校数学a 順列とは 練習編 映像授業のtry It トライイット




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説



確率問題全般 京極一樹の数学塾




同じものを含む順列の問題についてです この問題の のマーカーをした 数学 教えて Goo




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




同じものを含む順列と組合せは 同じ です 問題4選もあわせて解説 遊ぶ数学




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



場合の数 Of 京極一樹の数学塾会員頁




順列pと組み合わせcの違いと 簡単 な見分け方




高校数学のサイコロの問題と順列の問題と順列の利用 Clear




男子3人女子3人から 男女が交互になるように並ばせる円順列の問題なの 数学 教えて Goo



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



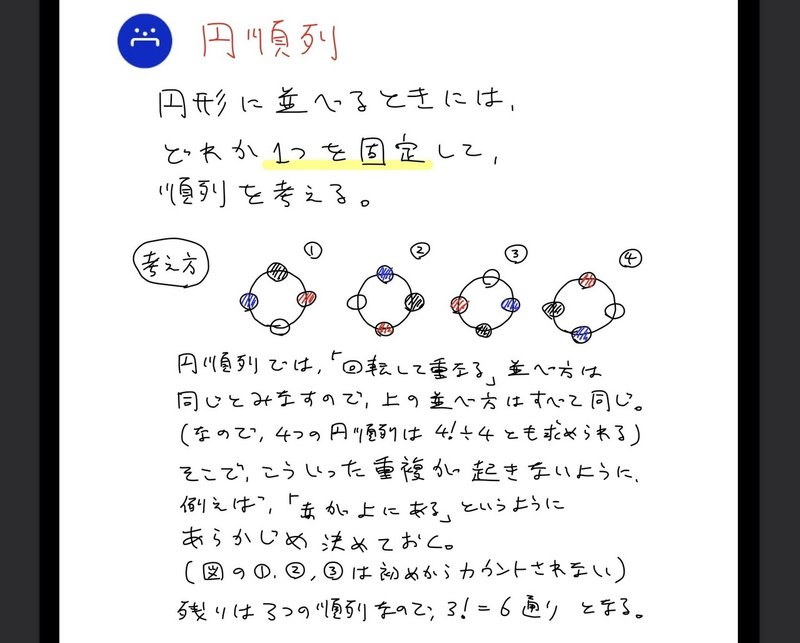
1




3講 順列 1章 場合の数と確率 問題集 高校数学a




高校数学a 順列の活用2 男女の並べ方 練習編 映像授業のtry It トライイット



やや難 数学入試問題




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com




重複順列とは 基本公式と解き方を解説 高校生向け受験応援メディア 受験のミカタ




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




高校数学a 重複順列 例題編 映像授業のtry It トライイット




順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング




高校用 トレーニングノートa順列と組合せ 数学a領域別 全国数学問題研究会 本 通販 Amazon




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列 組合せに頼らない 素朴に数える ための3本柱 わが子を算数 数学嫌いにさせない習慣 朝日新聞edua




3講 順列 1章 場合の数と確率 問題集 高校数学a



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




第6回 数学問題 順列を作る Dreamhanks Blog




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




数学aです 問題 Defenseの7文字から4文字を取り出す時 Eを3個含む場 高校 教えて Goo



重複順列 同じものを含む順列 数学入試問題




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




この問題で円順列かじゅず順列かどちらを使うかが見分けることが出来ません Clear



同じものを含む順列の問題 京極一樹の数学塾




高校数学a Npr と Ncr の使い分け 映像授業のtry It トライイット



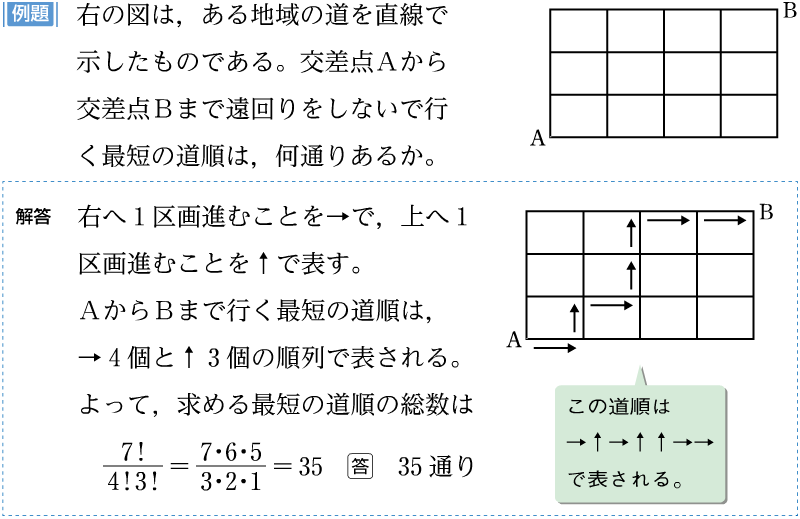
3



確率問題全般 京極一樹の数学塾




高校数学a 最短の道順の求め方 例題編 映像授業のtry It トライイット




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




順列と組み合わせ 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



教科書ガイド数研版 定期テスト対策問題 数学a 内容を見る




高校数学a 組合せの計算1 Ncr 例題編 映像授業のtry It トライイット




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




道順の場合の数を求めるテクニック 高校数学の美しい物語




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note



数学iaiib全問題 Ia 場合の数 確率




高校数学a 同じものを含む順列 練習編 映像授業のtry It トライイット




数学の順列の問題でよくある 仕切りを利用する問題で なぜ問題にはない仕切りを計算の中 Clear




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




高校数学 数a 勉強動画 順列 基本編の問題 19ch



3




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列の公式 証明と公式の意味 高校数学の知識庫
コメント
コメントを投稿